Читая об аэродинамике что-то более серьезное, чем мой сайт, вы наверняка сталкивались с математическими формулами, выглядящими весьма угрожающе. Впрочем, для некоторых из нас формулы — это вполне естественный способ познания окружающего мира. Должен признаться, что еще в школе я отчаянно завидовал таким людям, помнящим, что косинус 30 градусов равен «корню-из-трех-деленному-на-два», а синус этого же угла — «одной второй». Круче этого могло быть только знание количества диезов в тональности фа# мажор (которое я безуспешно пытаюсь запомнить всю жизнь).
Эта статья написана не для этих высоколобых «ботаников» и магистров точных наук, цитирующих на память любую страницу из таблицы Брадиса, а для нормальных людей, давно забывших то, чего никогда толком и не знали.
Помните анекдот? «Было у отца три сына: двое умных, а третий — летчик». Как водится, сказка ложь, да в ней намек: летчику, в отличие от, например, инженера, формулы не очень-то и нужны. Решать квадратные уравнения и брать интегралы в процессе полета удается немногим, а если и удается — то с большими ошибками и погрешностями.
Дело летчика не уравнения решать, а за ручки дергать и кнопки нажимать, нравится это ему или нет. Именно в этом заключается пилотирование воздушного судна. Много ли формул вы используете, ежедневно управляя автомобилем? Не ошибусь, если скажу, что ни одной. Да, конструкторы и инженеры использовали множество формул и выполнили массу расчетов при создании вашего авто (низкий им поклон). Но вы лишь наливаете в бак бензин, вставляете ключ в замок зажигания и давите на педали, то есть просто потребляете результат труда тех, у кого когда-то списывали на уроках математики.
Конечно, управление самолетом несколько сложнее, чем автомобилем, поскольку происходит не в двух, а в трех измерениях. Вдобавок, происходит оно непрерывно и безостановочно: нельзя включить указатель поворота и съехать на обочину, чтобы освежить в памяти некоторые теоретические знания или получше обмозговать возникшую проблему. Оторвавшись от земли, пилот вынужден без передышки, в течение всего полета оперативно решать задачи и искать ответы на непрерывно возникающие вопросы, а также выполнять некоторые расчеты. Единственный способ делать это быстро — отказаться от точных вычислений, иногда сводя расчеты буквально к прикидкам «хрен к носу».
Зачем же тогда летчику вообще эти страшные формулы? Лишь для понимания происходящих в полете процессов (зачастую невидимых) и, главное, способов воздействия на них. Ведь если повлиять на процесс все равно невозможно, то и знание формулы бесполезно! Хорошая новость состоит в том, что количество процессов, на которые летчик может влиять, весьма ограничено. Значит, и нужных нам формул не так уж много.
Ниже я привожу только те формулы, законы и графики, знакомство с которыми делает управление самолетом более осмысленным, а значит, безопасным. Вы увидите, что они достаточно просты и немногочисленны. Постарайтесь если не понять, то хотя бы запомнить, что они существуют — и тогда вы сможете принимать верные «управленческие решения» в полете.
Начнем, само собой, с основы основ: формулы подъемной силы. Ведь это именно то, что держит самолет в воздухе. Неглупо знать, от чего она зависит и как можно менять ее величину в полете. Итак,
ПОДЪЕМНАЯ СИЛА, Y: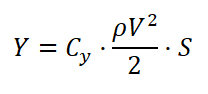
Здесь Cy — коэффициент подъемной силы, ρ — плотность воздуха, V — скорость и S — площадь крыла.
«Постойте!» — скажете Вы, «Я точно знаю, что подъемная сила зависит от угла атаки. Да мне об этом все уши прожжужали! Где он в этой вашей формуле?» — и будете совершенно правы.
Действительно, подъемная сила зависит от угла атаки, и в этой формуле с ним вышло так же, как с тем сусликом, которого не видно, но он — есть. Дело в том, что от угла атаки меняется коэффициент подъемной силы Cy, который и представлен в этой формуле. То есть, для каждого угла атаки профиля существует свой собственный коэффициент Cy, определить который можно эмпирически.
Обычно это делают в процессе испытаний (продувки профиля в аэродинамической трубе или методом математического моделирования), а затем полученные значения наносят на графики и таблицы зависимости Cy от α. Нам, пилотам, эти конкретные значения сообщают редко. А зачем они нам? Все, что нам положено знать, это: Cy растет при увеличении угла атаки α, а вместе с ним растет и сама подъемная сила.
Ну хорошо, с углом атаки разобрались. А какие еще параметры мы можем изменить в полете, чтобы увеличить или уменьшить подъемную силу?
Давайте еще раз посмотрим на формулу. Скажем, можем ли мы как-то влиять на плотность воздуха ρ? Для этого пришлось бы быстро и существенно изменить высоту полета или температуру окружающего воздуха, а это сделать нереально. Значит, забудем про эту переменную.
А что с площадью крыла S? Что, если мы ее увеличим, выпустив закрылки или предкрылки? Сама по себе мысль здравая: действительно, выпуск закрылков или предкрылков увеличивает эффективную площадь крыла, что влечет за собой рост подъемной силы. Однако выпуск механизации повлияет и на эффективный угол атаки из-за изменения наклона хорды профиля. Да и длина самой хорды увеличивается! По сути, выпуск механизации дает нам другой профиль крыла. Сравнивать несущие свойства двух различных профилей было бы неправильно.
Выходит, что говорить об изменении площади крыла S за счет использования механизации не корректно с точки зрения аэродинамики? Да, это так. Но если честно, в полете подобные тонкости нас не особо волнуют. Поэтому мы можем условно считать выпуск механизации средством увеличения подъемной силы.
Что же еще осталось в этой формуле? А осталось самое главное — скорость V. Главное потому, что, во-первых, пилот может влиять на нее в очень широких пределах, а во-вторых, как мы видим, увеличение подъемной силы пропорционально квадрату скорости. Из чего можно сделать вывод, что этот способ изменения подъемной силы в полете является наиболее эффективным (быстрым). Скорость является необходимым условием создания достаточной подъемной силы и одним из ключевых факторов безопасности полета. Пилоту следует внимательно следить не только за текущим значением, но и за тенденциями изменения скорости, с тем чтобы корректирующими действиями упреждать ее выход за допустимые значения.
ЛОБОВОЕ СОПРОТИВЛЕНИЕ, X: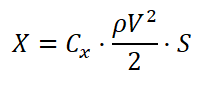
Просто дежавю, не так ли? Те же ρ, V и S… И коэффициент Cх — коэффициент лобового сопротивления — подозрительно похож на Cy , который мы видели в формуле подъемной силы выше. Может быть, он тоже зависит от угла атаки? Точно! Зависит. И точно также каждому углу атаки соответствует свой коэффициент лобового сопротивления Cх, значения которого определяются в результате продувки профиля крыла или модели самолета в аэродинамической трубе и наносятся на всевозможные графики и таблицы, используемые инженерами-конструкторами.
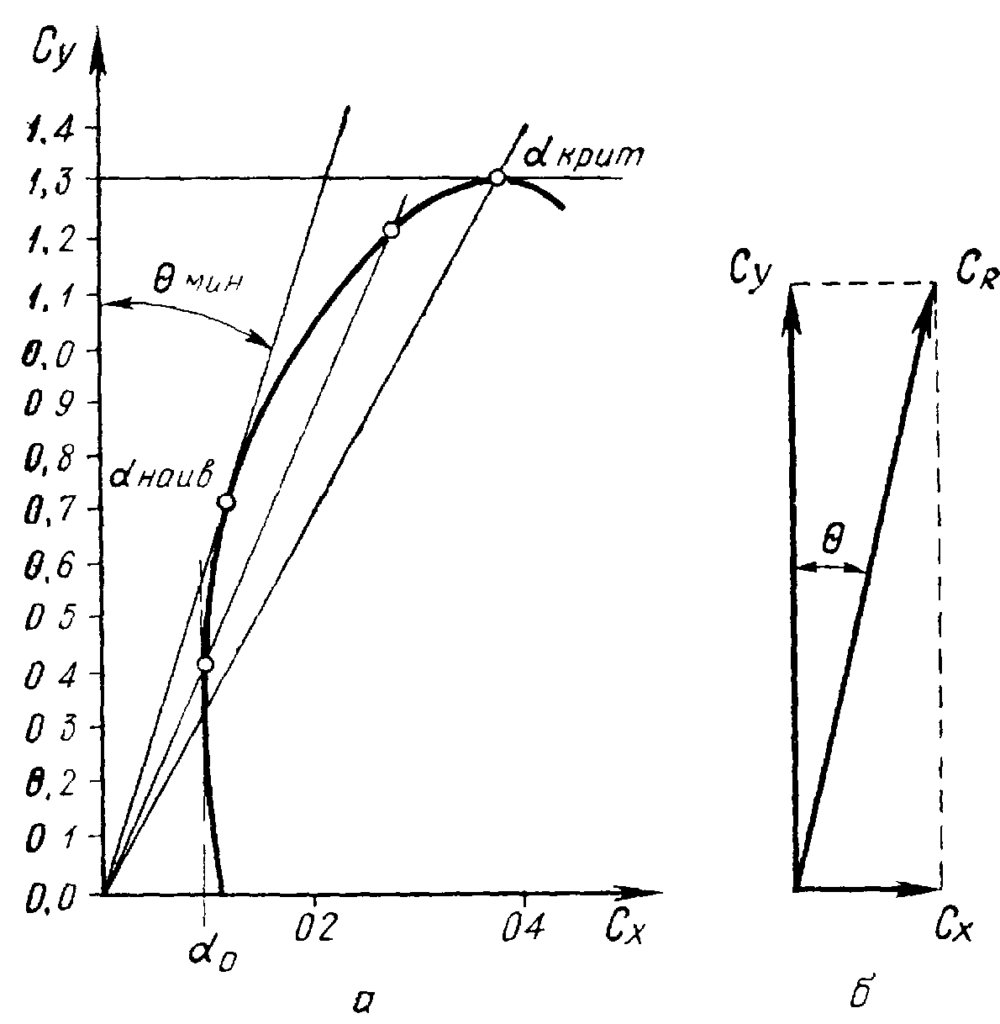
Впрочем, при удаче, в специализированной литературе и некоторых руководствах по летной эксплуатации можно видеть такой специфический вид графика, как «поляра». Такие графики часто используются в аэродинамике и представляют из себя графическую зависимость одного параметра от другого, ему подобного. В данном случае, это как раз зависимость Сy от Cх.
ПОЛЯРА ПРОФИЛЯ:
Хотя на поляре изображают взаимосвязь коэффициентов подъемной силы и лобового сопротивления, можно сказать, что данная кривая графически отражает взаимосвязь самой подъемной силы (ось Y) и силы лобового сопротивления (ось X), формулы которых мы рассмотрели выше. Эта взаимосвязь индивидуальна для каждого профиля или типа самолета и отражает их аэродинамическое совершенство, или качество.
КАЧЕСТВО САМОЛЕТА: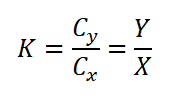
Отношение Y/X, как и отношение соответствующих им коэффициентов Cy/Сx, называется аэродинамическим качеством K, графическим выражением которого и является поляра.
Отдельно следует отметить, что на поляре существует точка, где отношение Cy/Сx максимально, а значит, и качество K — максимально. Графически эта точка находится проведением касательной из центра координат к поляре:
Угол атаки, соответствующий полету с максимальным качеством, называется наивыгоднейшим, а угол θ мин между касательной и осью ординат является минимальным углом наклона траектории при планировании.
Помимо касательной, можно провести и другие прямые из центра координат, секущие поляру в двух точках. Это означает, что у самолета могут существовать два различных угла атаки, при полете на которых достигается одинаковое аэродинамическое качество и угол наклона траектории.
ОДНАКО, только на наивыгоднейшем угле атаки обеспечивается максимальное качество и минимальный наклон траектории снижения, то есть максимальная дальность планирования (весьма важная при отказе двигателя).
УГОЛ НАКЛОНА ТРАЕКТОРИИ:
Различают два вида снижения: простое планирование и моторное снижение (когда силовая установка создает некоторую тягу).
Для прогульщиков геометрии в школе, напомню: чем больше значение тангенса угла, тем больше сам угол, и наоборот.
Как следует из формулы, значение тангенса угла наклона траектории обратно пропорционально качеству: чем выше качество, тем оно меньше. Значит, чем выше качество, тем более пологой будет траектория снижения и больше дальность планирования.
При моторном снижении к вышесказанному добавляется влияние тяги. Согласно формуле, увеличение тяги приводит к уменьшению значения тангенса (выражение P/G имеет отрицательный знак). Значит, чем больше тяга, тем более пологой будет траектория и больше дальность планирования.
Вес G, как вы заметили, присутствует только в формуле моторного снижения и то в качестве «понижающего коэффициента» для воздействия тяги. Действительно, чем тяжелее самолет, тем большая потребуется тяга для того, чтобы уменьшить наклон его траектории снижения на заданный угол.
ПРАКТИЧЕСКИЙ ВЫВОД: при заходе на посадку углом наклона траектории (вертикальной скоростью) управляют именно изменением тяги двигателя и/или увеличением аэродинамического сопротивления. Изменение тангажа используется для управления воздушной скоростью, а не для изменения траектории. Как только рекомендованная скорость получена и самолет стриммирован на данном угле атаки, перелет / недолет следует исправлять режимом двигателя, а не игрой в «тяни-толкая» со штурвалом. Дополнительно можно использовать выпуск шасси, закрылков и перевод винта на малый шаг в качестве средств увеличения аэродинамического сопротивления, что ведет к ухудшению качества и, таким образом, обеспечивает более отвесную траекторию снижения.
НЕОЖИДАННЫЙ ВЫВОД: сам по себе вес самолета никак не влияет на траекторию снижения и дальность планирования. То есть более тяжелый самолет на том же угле атаки будет планировать также далеко и полого, что и более легкий. Удивительно, да? Как же такое может быть, спросите вы? Просто более тяжелый самолет будет лететь быстрее и окажется на земле раньше. Природа увеличения потребных скоростей полета лежит за рамками этой статьи, но если любопытно, то поищите информацию о сдвиге кривых потребных тяг и мощностей при увеличении веса самолета. А пока важно поверить формулам и запомнить, что вес не влияет на наклон траектории планирования.
ТЯГА СИЛОВОЙ УСТАНОВКИ:
Раз уж мы заговорили о тяге, давайте поймем, что это такое. Прежде всего, P (тяга) — это сила. Понимание этого факта весьма полезно, т.к. согласно второму закону Ньютона, F=ma. То есть, сила равна произведению массы на ускорение. А теперь давайте посмотрим на формулу, объясняющую природу силы тяги:
Здесь m — масса, Vвых и Vвх — скорости воздуха перед и позади силовой установки, t — время.
Как работает авиационная силовая установка? Очень просто: в каждую единицу времени она на некоторую величину изменяет скорость воздуха определенной массы. Грубо говоря, пропеллер «засасывает» воздух перед собой и отбрасывает назад, сообщая ему ускорение. Так как воздух имеет массу, то все получается в точности по Ньютону: сила тяги равна массе воздуха, умноженной на сообщенное ему ускорение. Вуаля!
На практике, увеличивая обороты двигателя (и винта) мы одновременно увеличиваем и массу воздуха, и сообщаемое ему ускорение, что обеспечивает значительное изменение величины тяги между малым газом и взлетным режимом.
МОЩНОСТЬ СИЛОВОЙ УСТАНОВКИ:
Здесь кроется одна тонкость, вызывающая как смуту в головах пилотов всех стран и народов, так и жаркие баталии диванных аэродинамиков в многочисленных форумах и чатах. А причиной тому — формула мощности силовой установки:
Как видим, мощность — это произведение тяги на скорость самолета (sic!). Здесь крайне важно увидеть, что если скорость самолета равна нулю, то и мощность равна нулю, хотя тяга при этом может быть максимальной. Как же так? А вот так!
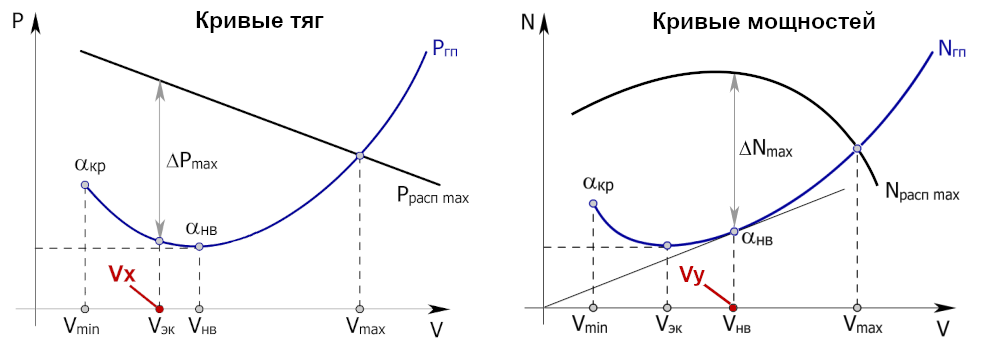
Вообще, мощность — это мера того, как быстро совершается работа. Если тело неподвижно, то никакой работы по его перемещению не совершается, и расходуемая мощность равна нулю. Этот нюанс действительно стоит запомнить и, в дальнейшем, всегда разделять тягу и мощность, а также их графики. Например кривые Жуковского для тяг и мощностей на рисунке ниже имеют разную форму в силу своей разной природы. Вдобавок пропорциональны квадратичной и кубической функции, соответственно.
Еще одним важным нюансом является вот что: во многих учебниках и руководствах вы будете встречать формулу мощности, выглядящую вот так: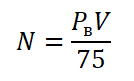
Эта формула абсолютно верна, но дается для получения мощности не в Ваттах, как теперь положено в Международной системе единиц (СИ), а в лошадиных силах. При выполнении расчетов для ее корректного применения необходимо использовать значение тяги P не в Ньютонах, а в килограмм-силах, кгс. Использованием этой единицы измерения силы и объясняется наличие числа 75 в знаменателе данной формулы.
ТЯГА И МОЩНОСТЬ — ЭТО «ДВЕ БОЛЬШИЕ РАЗНИЦЫ»
Хотя и тяга, и мощность зависят от скорости, их физическая природа различна. Поэтому, а также в силу падения располагаемой тяги поршневой силовой установки с ростом скорости, максимальный запас тяги (ΔP max) и максимальный запас мощности (ΔN max) воздушного судна существуют при различных скоростях полета. А так как скорость максимального угла набора высоты (Vx) достигается при максимальном запасе тяги, а скорость максимальной скороподъемности (Vy) — при максимальном запасе мощности, то именно различием между тягой и мощностью и объясняется различие значений этих важнейших скоростей (см. графики кривых тяг и мощностей выше).
РАДИУС РАЗВОРОТА
Радиус разворота зависит одновременно и от воздушной, и от угловой скорости движения самолета. Впрочем, это характерно для любых движущихся тел. Вот представьте, к примеру, что вы участвуете в кольцевых гонках на мотоцикле. Можно было бы снижать скорость на виражах, но ведь так гонку не выиграть! Вместо этого приходится наклонять мотоцикл на очень большой угол (да так, что иногда из-под него искры летят). Только так можно увеличить угловую скорость (т.е. уменьшить радиус виража), не снижая скорости движения мотоцикла.
То же самое происходит и с самолетом: хотите выполнить вираж ‘покомпактнее’, в пределах какой-нибудь тренировочной зоны или внутри горного каньона — снижайте скорость либо заламывайте большой крен. Но только помните, что и то, и другое действие приближает самолет к скорости сваливания! Первое — очевидно: чем меньше воздушная скорость, тем меньше запас до опубликованной скорости Vs. Однако, увеличение крена означает рост перегрузки и увеличивает скорость сваливания (объяснение см. ниже). Получается, что в данной ситуации значения текущей воздушной скорости и скорости сваливания движутся навстречу друг другу. Если позволить им встретиться, выполняя полет на малой высоте, то тут одними только искрами уже не обойдется…
Если вы когда-нибудь из чистого любопытства захотите вычислить радиус виража, то вот вам формула. Выраженный в метрах, он равен квадрату воздушной скорости в км/ч, делённому на произведение константы 126.63 и тангенса угла крена γ.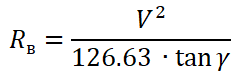
НОРМАЛЬНАЯ ПЕРЕГРУЗКА
Еще одной характеристикой, от которой очень многое зависит в полете, является нормальная перегрузка, ny. Вообще говоря, нормальная перегрузка — это лишь один из компонентов полной перегрузки, действующий вдоль вертикальной (нормальной) оси самолета oY. А полная перегрузка — это отношение суммы полной аэродинамической силы и силы тяги к весу самолета, n=(R+P)/G.
Что это вообще такое, перегрузка? Многие думают, что перегрузки возникают лишь в критических ситуациях в полете, в тот самый момент, когда «в кабине запахнет мужеством». Но на самом деле, перегрузка незримо сопутствует всему полету, с самого начала и до конца. Просто большую часть времени все силы, действующие на самолет, сбалансированы и перегрузка равна 1, своему обычному «земному» значению. Поэтому мы ее и не замечаем. В остальное время летчики стараются пилотировать самолет так, чтобы не только не превышать допустимые ограничения самолета по перегрузке, но и обеспечить достаточный комфорт пассажиров, и не допускают существенного ее нарастания.
Вообще, изменение перегрузки — это неизбежный эффект, возникающий в результате искривления траектории движения тела. На самом деле, перегрузку можно ощутить и на земле, например, при движении в автомобиле или поезде. Когда они тормозят, разгоняются или поворачивают, на них (и на наше тело) действует перегрузка, которую легко заметить: нас бросает вперед при торможении, вжимает в кресло при разгоне или прижимает к двери автомобиля в крутом вираже. Это и есть увеличение перегрузки от 1 до некоторого, иногда весьма существенного, значения, которое мы видим, например, здесь:
Всего у полной перегрузки, действующей на самолет, три проекции: продольная (на ось X), поперечная (на ось Z) и нормальная (на вертикальную ось Y). Продольная и поперечная перегрузки, действующие на большинство транспортных самолетов, сравнительно невелики и, поэтому, их обычно оставляют без рассмотрения. Хотя если вы планируете использовать форсаж или садиться на палубу авианосца… Ну, да ладно, вернемся лучше к реальности и рассмотрим оставшуюся, нормальную перегрузку.
Эта перегрузка действует вдоль той же оси Y, что и подъемная сила, и является продуктом ее создания. Вот смотрите: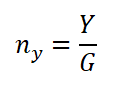
Все очень просто: изменяя подъемную силу мы увеличиваем или уменьшаем нормальную перегрузку. А что является одним из наиболее оперативных способов изменения подъемной силы? Верно, увеличение угла атаки. Поэтому не будет большим преувеличением сказать, что каждый раз, когда нам приходится увеличивать подъемную силу взятием штурвала на себя, мы увеличиваем перегрузку. А когда это приходится делать?
По сути, основных случаев для такого действия три: вывод из пикирования, ввод в горку и выдерживание высоты при выполнении виражей. И во всех этих трех случаях существует опасность превысить либо критический угол атаки (тогда самолет свалится), либо эксплуатационное ограничение по перегрузке (тогда самолет сломается). Ваш выбор!
Если же говорить серьезно, то ни того, ни другого допускать нельзя. Надо внимательно относиться к перегрузке и хорошо себе представлять, когда она возникает. Попросите инструктора показать вам перегрузки большой величины, например, при выводе из крутой спирали или штопора, для того чтобы знать, как они ощущаются, и научиться определять их величину без прибора-акселерометра. Это поможет вовремя отмечать их рост при выполнении маневров и не допускать выхода за допустимые значения. Кроме того, большая (но допустимая) перегрузка, возникающая при выводе из крутого пикирования, может испугать неподготовленного летчика. Стараясь ее уменьшить до более комфортной величины, он может отпустить штурвал и допустить значительную потерю высоты, опасную столкновением с землей.
ЗАВИСИМОСТЬ ПЕРЕГРУЗКИ ОТ УГЛА КРЕНА
Я подробно рассказал о возникновении перегрузки при выполнении разворотов и виражей в другой статье на этом сайте. Здесь же я лишь хочу напомнить соответствующую формулу и подчеркнуть, что в вираже перегрузка любого самолета не зависит ни от чего иного, кроме угла крена γ, то есть ни вес, ни скорость на нее не влияют: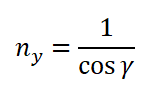
Есть один важный нюанс, о котором, почему-то, забывают даже очень квалифицированные летчики и инструкторы. Эта формула справедлива ТОЛЬКО в случае, если вираж выполняется на постоянной высоте. Если же самолет будет снижаться, то перегрузка уменьшится. Правда за это придется заплатить существенной потерей высоты, но тут уж ничего не поделать, или — или.
Теперь, когда мы разобрались с самой перегрузкой и с тем, как именно мы можем ей физически управлять в полете (напомню для забывчивых: штурвалом!), стоит упомянуть о том, как она влияет на потребную тягу и мощность в вираже. Если такой вираж производится без снижения, то, как нетрудно догадаться, потребуются большая тяга и мощность.
ТЯГА, ПОТРЕБНАЯ ДЛЯ ВИРАЖА:
Здесь видно, что перегрузка, возникающая в вираже, является повышающим коэффициентом для потребной тяги. Так, выполняя вираж с креном 60°, перегрузка в котором равна 2, нам потребуется вдвое большая тяга, чем в горизонтальном полете.
Важно знать, что данная формула имеет больше теоретическое, чем практическое значение: она предполагает, что вираж выполняется на том же угле атаки, на котором самолет выполнял горизонтальный. Для этого требуется увеличение скорости полета в вираже для получения большей подъемной силы. В реальности же глубокие виражи обычно выполняются без увеличения скорости, но на большем угле атаки, чем угол горизонтального полета. Это требует несколько меньшего прироста тяги, но уменьшает запас по скорости и углу сваливания в вираже, о чем обязательно следует помнить летчику.
МОЩНОСТЬ, ПОТРЕБНАЯ ДЛЯ ВИРАЖА: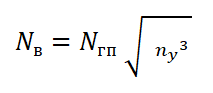
Как и в случае с потребной тягой, здесь предполагается увеличение скорости полета для выполнения виража на том же угле атаки, на котором самолет летел до начала виража. А так как мощность — это произведение тяги на скорость, а в данном случае — увеличенной тяги на увеличенную скорость, мы получаем такую интересную формулу. Теперь, если бы мы выполняли тот же самый вираж с креном 60° и перегрузкой 2, потребная мощность увеличилась бы в «корень квадратный из перегрузки в кубе» (как звучит, а?), то есть в 2.83 раза! При дальнейшем увеличении крена она увеличивается настолько стремительно, что делает невозможным выдерживание скорости и высоты полета из-за возникающего дефицита располагаемой мощности.
ВЫВОД: «КРЕН МОЙ — ВРАГ МОЙ». При нормальном маневрировании следует избегать больших кренов, так как они неизбежно ведут к потере высоты или скорости, что представляет угрозу для безопасности полета.
ВЛИЯНИЕ ПЕРЕГРУЗКИ НА ПОТРЕБНЫЕ СКОРОСТИ
Рост перегрузки увеличивает потребные скорости полета в «корень из перегрузки раз». Почему это происходит? Для увеличения перегрузки требуется большая подъемная сила, а для создания последней требуется либо большая скорость, либо угол атаки. В последнем случае уменьшается запас по углу атаки, что вновь проявляется в увеличении скорости — на этот раз скорости сваливания. Справедливо и обратное: уменьшение перегрузки уменьшает потребные скорости полета.
ПОТРЕБНАЯ СКОРОСТЬ ВИРАЖА: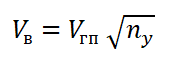
Все просто: для выполнения виража на том же угле атаки, на котором выполнялся горизонтальный полет, надо, зная угол крена, определить перегрузку в вираже, а затем взять из нее квадратный корень и умножить скорость горизонтального полета на получившееся значение.
СКОРОСТЬ СВАЛИВАНИЯ ПРИ КРЕНЕ:
Эта формула имеет самое практическое значение. По ней можно рассчитать, как увеличивается скорость сваливания в зависимости от величины крена в вираже, выполняемом с сохранением или набором высоты. Зная угол крена, определяем перегрузку, берем из нее квадратный корень и умножаем опубликованную в РЛЭ скорость сваливания на полученный результат.
ВАЖНО: как вы помните, в РЛЭ публикуется скорость сваливания Vs без крена. Та же самая скорость соответствует нижнему концу зеленой или белой (с закрылками) дуги на указателе скорости. Однако при любом значении крена, отличном от 0, скорость сваливания увеличивается. И делает она это в полном соответствии с формулой, которую вы здесь видите. При кренах, больших 30°, перегрузка начинает стремительно нарастать, что существенно увеличивает скорость сваливания.
ЭВОЛЮТИВНАЯ СКОРОСТЬ: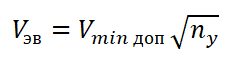
Эволютивной скоростью называется наименьшая скорость в процессе выполнения маневра, при которой еще обеспечивается безопасное его завершение. На практике, производитель самолета или авиакомпания определяет некоторый угол атаки α доп, полет на котором признается безопасным (т.е. гарантирующим от сваливания). Выполнение полета на большем угле атаки не допускается.
Так как в большинстве случаев летчик пилотирует самолет не по указателю угла атаки, а по приборной скорости, ему нужно знать то значение воздушной скорости, на котором будет достигнут этот допустимый угол. Не было бы ничего проще, если бы потребные скорости полета на заданном угле атаки не росли с увеличением перегрузки. Как мы знаем, при любом маневрировании самолета перегрузка будет отличной от 1, а значит, и минимально допустимая скорость изменится.
В связи с этим поступают следующим образом: по вышеприведенной формуле определяют скорость с учетом фактической перегрузки при выполнении каждого заданного маневра (например, на восходящем участка петли перегрузка ny=4) или используют такое ее максимальное значение, которое может возникать в нормальном полете (≈1.5 для транспортных самолетов).
Например, взяв квадратный корень из 1.5 мы получим «повышающий коэффициент» 1.22, на который следует умножить заданную минимально допустимую скорость горизонтального полета Vmin доп. В результате мы получим эволютивную скорость, Vэв, являющуюся нижней границей диапазона скоростей, разрешенных для пилотирования данного воздушного судна. Эта скорость может быть внесена в РЛЭ или в Руководство по Производству Полетов (РПП) авиакомпании.
РАСЧЕТ СКОРОСТИ ЗАХОДА (Vref) В ЗАВИСИМОСТИ ОТ ВЕСА
Вообще, вес самолета влияет не только на скорость захода, но и на ряд других скоростей, таких, как скорость сваливания, наивыгоднейшая, экономическая и крейсерская скорости и т.д. Это происходит потому, что вся кривая потребной тяги сдвигается вправо с увеличением веса и влево — с его уменьшением.
Важно понимать, что скорости, которые публикуются в РЛЭ, даются для максимального взлетного веса. Увеличение этих скоростей с увеличением веса верно аэродинамически, но идет вразрез с правилами эксплуатации авиатехники: взлет с превышением максимального взлетного веса категорически запрещен. Поэтому на практике мы используем данную формулу только для расчета потребных скоростей при уменьшенном весе. Это, если хотите, «формула недогрузки». Рассмотрим ее на примере расчета рекомендованной скорости захода на посадку Vref: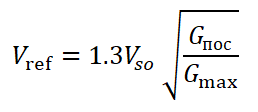
Здесь Gпос — вес самолета на заходе на посадку, Gmax — максимальный взлетный вес, Vso — скорость сваливания в посадочной конфигурации при максимальном взлетном весе.
Как мы видим, если посадочный вес равен максимальному взлетному весу, то отношение весов даст нам 1, корень квадратный из которой — тоже 1. Таким образом, скорость захода на посадку будет равна 1.3 от Vso, что и является оптимальной скоростью самолета на короткой прямой.
Часто РЛЭ рекомендует несколько иное значение скорости захода. В таком случае, просто подставьте это значение в формулу вместо 1.3Vso и вы сможете скорректировать эту скорость под уменьшенный вес. Например, если летите на более легком самолете в варианте загрузки «курсант + инструктор».
Аналогично, подставив другие опубликованные в РЛЭ скорости вместо выражения 1.3Vso, можно найти скорости Vs, Vэк, Vнв, Vx, Vy, Va и Vкр (крейсерскую, если опубликована) для облегченного самолета. Только не корректируйте такие скорости, как Vno, Vne и Vb, которые назначаются, в том числе, исходя из ограничений по прочности конструкции планера. Пусть конструкторы несут ответственность за эти ограничения. Наше дело им строго следовать.